그래프 이론

이거 캠에 잘 나왔는데?

1. 그래프 SMILES에서 조금 나온 그래프는 꼭대기와 변을 통하고 있는 객체 간 연결 관계를 나타내는 것이다.그 자체로 어떠한 정보를 전할 수도 있다.주가 그래프는 한강의 물의 온도를 체크하고 꺾은 선 그래프나 막대 그래프나…이래봬도 선생님, 그 그래프가 아닙니다.여기서 말하는 그래프는 “일부 객체의 페어가 서로 관련하는 객체의 집합을 이루는 구조”이라 정의합니다.정점(V)와 변(E)의 순서쌍 집합에 의한 G=(V, E)로 정의하지 않나!!!참고로, 저것은 츄쯔훌이야.도대체 왜 딥 러닝 관련 논문을 보면 층간의 연산 이동(과잉 가중치)을 마루(화살표로 나타내고 있지만, 그것도 일종의 그래프이다.노드가 정점에서, 각층으로 향하는 화살표가 근처.변이 화살표라 유향 그래프이다.그런데 딥 러닝 관련 논문을 그렇게 많이 보는 것도 아닌데… 그렇긴거기에서 예제를 준비했다.

7호선이 석남까지 이어지지 않는 것을 보면이것도 좀 올드인데…이래봬도알 〇 올든 곳까지 가면어떻게 치냐고?초등 학생 때는 온수행은 뭐야, 7호선 종점 건물 크기였다.그때는 원흥 역도 없었고, 6호선도 없었다···중앙 선인가요?아니, 없었는데?중앙선상 오토리 역이나 고교 졸업하고 생겼어. 아마···경의선도 쟈쵸루 아니라면… 그렇긴지금은 쟈쵸루지만.그때는 하남시도 지하철로 갈 수 없었지만, 지금은 연결되었습니다.아니, 그래프의 이야기를 하는 거기에 지하철 소리예요… 그렇긴저것도 일종의 그래프이다.내가 봐도 좀 복잡하지 않나!!!정말 이 상태로는 수도권은 지하철로 연결될지도…이래봬도나중에 경기도화 성에도 지하철 역이 할 수 있잖아?이미 소동탄 역이 있는데, 어쨌든… 그렇긴6호선에는 저기 버뮤다 타카 이와치대가 있다.(저기에 화살표가 있는 것이 그 부분은 유카 같은데?)기본적으로 그런 노선도는 무당 향에서 지하철 역마다 있는 그 문장에 타면 어디 가느냐가 적힌 노선도는 화살표만 없고, 진행 방향은 있으니까 아마 유카다.노선도는 일단 정점으로 변으로 이루어졌으며 각 역의 연결 관계를 보였다.(물론 실제 지형을 반영 안 한대요)자 보세요.내가 오랜만에 스 서울에 상경한 친구랑 맛있는 것을 먹으러 강남 간다.그런데 내가 지금 있는 곳이 성수 역이야.그럼 2호선 강남 역에 가야 하는데 이 경우 노선도를 통해서 얻어지는 정보가 2개이다.첫째는 어느 순환선에 타면 빨리 도착하나(2호선은 외근/집안으로 구성되어 있어 신설동/까치 산행키는 그것을 타고 역에서 선로가 나뉜다), 두번째는 가장 빠른 순환선을 타고 몇 정거장 정도 가면 좋을까.

이것도 일종의 그래프이다.그런데 그것은 내 집에 가는 버스가 아닌데?아무튼…이래봬도정류소가 정점, 다음 정류장까지 연결 관계가 변수 곡선이며, 지하철 노선도와 마찬가지로 여기서 저기까지 몇 역이나(+방향)을 볼 수 있다.방향이 어지러울 때는 네이버 지도 않나!!!참고로 정류소 이름이 같아도 ID가 달라서 잘 보고 탄다.우리 동네 버스 정류장의 ID는 기억하는 것도 있고… 그렇긴내가 31년 동안 살고 있지만, 정류소 위치도 모르고…이래봬도집에서 조금 걸으면 중학교도 나오는 거… 그렇긴 아직 있습니다그 지옥의 경사에서… 그렇긴소방서와 경찰서도 있다…(경찰서는 리모델링을 한번 한다)2. 그라프 이론 용어, 일단 최대한 간결하게… 그렇긴그림 해설을 붙여서 설명할 예정이지만 그래도 어렵다.어려우면 정상이다.나도 그렇다면… 그렇긴

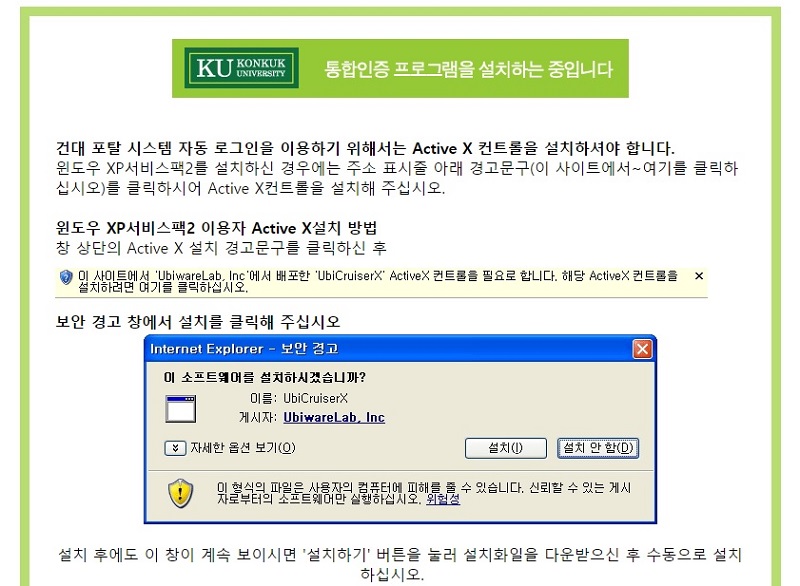
*차수 : d(v)로 표기하고 그래프의 정점을 연결하는 변의 수를 나타낸다. 무향 그래프는 위 그림과 같이 그대로 차수로 나누는데, 유향 그래프의 경우 입차수 출차수가 따로 있다. (입차수: 화살표 머리가 해당 꼭짓점을 향하는 것/출차수:해당 꼭짓점에서 화살표가 출발하는 것) *유향/무향:변이 화살표이면 유향(방향 있음), 단지 선이라면 무향(방향따윈 없어) *꼭짓점:그래프의 노드*변:노드를 연결하는 선

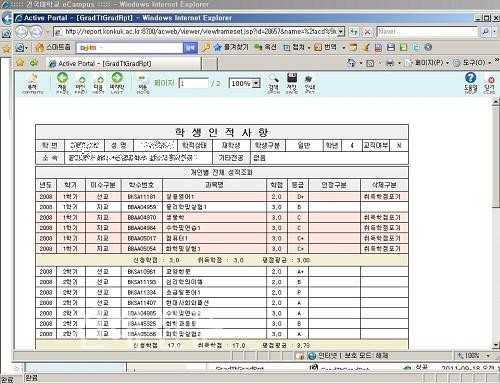
*전역목(부분 신장 그래프, spanning tree) : 어떤 그래프의 부분 그래프(어떤 그래프의 정점과 변의 일부 포함)이면서 그 그래프의 정점을 모두 포함하는 그래프(위 그림을 보면 변 하나가 빠졌다) *하중 그래프: 말 그대로 하중이 붙어 있는 그래프. 딥러닝의 모식도도 하중 그래프이다. 노선도에 비유하자면, 각 정류장별로 이동하는 데 소요 시간이 걸린 노선도. (성수에서 강남까지 가는데 버스정류장당 몇 분 걸려?) 그 정도면 친구를 성수역이라고 부르면 되는데*극점:어느 정도의 양 종착*인접:두 변의 같은 정점에 연결되어 있을 때,”인접”으로 알려졌다.어린이 대공원 역과 중곡 역은 모두 군자 역에 연결되어 있기 때문에 인접한 관계.*길이:어느 정점에서 다른 정점까지 연결한 변의 개수(어린이 대공원 역에서 나가이와까지 몇 정류소?)*거리:어느 정점에서 다른 꼭짓점까지의 최단 거리(어린이 대공원 역에서 사슴 차례 역까지 최단 경로)록번 역에 뭔가 있지만오빠의 식당입니다사장, 소문을 듣고 오세요.유림 닭 하나 주세요.가능?엄마에게 드롭 킥할 것 아니냐.*지름:diam(G)로 표기.그래프의 최대 정점 간 거리를 의미한다.3호선의 대화 역에서 오금 역까지의 거리.6호선은 무엇으로 재어?저기 매 이와치대 끝에 있는 있어?그리고 7호선은 장암-건물 크기로 장암-온수로, 장암-부평구청이었으나 장암-석남이 됐다.*루프:근처의 두 정점이 동일한 것(그래서 자신과 관련되어 있는 것)재귀 함수 같은 거예요?그것은 무엇입니까?*다중쯤:정상 사이에 변이가 두개 이상 있는 것 멀티?*단순/다중 그래프:루프, 다중 변이 없는 그래프를 단순 그래프라는 루프, 다중 변이 있는 그래프를 다중 그래프.*극점: 어느 변의 양 종점*인접: 두 변과 같은 정점에 연결되어 있을 때 ‘인접한다’고 한다. 어린이대공원역과 중곡역은 모두 군자역으로 연결되어 있어 인접한 관계. * 길이 : 어느 정점에서 다른 정점까지 연결한 변의 개수(어린이대공원역에서 장암까지 몇 정거장?) * 거리 : 어느 정점에서 다른 정점까지의 최단거리 (어린이대공원역에서 녹번역까지의 최단경로) 녹번역에 뭔가 있습니다만 오빠네 식당입니다. 사장님 소문 좀 듣고 오세요.유림계 하나 주세요.가능? 엄마에게 드롭킥 되는 것은 아닌지 * 지름 : diam(G)로 표기. 그래프의 최대 정점간 거리를 의미한다. 3호선 대화역에서 오금역까지의 거리. 6호선은 뭘로 재요 저기 응암지대 끝에 있는 저거? 참고로 7호선은 장암-건대로 장암-온수로 장암-부평구청이었으나 장암-석남이 되었다. *루프:변의 두 꼭짓점이 동일한 것(그러니까 자기 자신과 연결되어 있는 것) 재귀함수 같은 것입니까, 그것은 무엇입니까? *다중변: 꼭짓점 사이에 변이가 둘 이상 있는 것 멀티인가. *단순/다중 그래프: 루프나 다중 변이가 없는 그래프를 단순 그래프라고 하며, 루프나 다중 변이가 있는 그래프를 다중 그래프라고 한다.대충 이런 식으로 도식화한다고 생각하면 된다.(SMILES에 예시도가 있다)정점이 원자, 변이 결합인데, 이중 결합은 그렇게 표시하는 것이 아니라 아래의 예처럼 근처에 하중을 주고 구별한다.Charge의 한 이온 형태에 드는 것은 변이가 없다.정점의 가장 바깥쪽 전자에 대한 정보와 편의 하중을 가하고 남는 전자는 스스로 암묵적으로 수소가 추가된다.그래서 SMILES에서 이온 표시하지 않고 O만 사용하면 물이 된다.위: cTAB(세트리모늄 브로마이드, 비누지만 DNA를 뽑을 때 많이 사용한다) 아래: 아세틸콜린(신경전달물질) 시탭은 비연결그래프(저기 브로민이 떨어져 있다), 아세틸콜린은 연결그래프다. 근데 이중결합도 있는데 왜 단순하냐고? 저기 예를 보면 주변에 숫자가 붙어 있을 거야. 결합을 변수가 아닌 변에 하중을 가하여 표현하였다. 꼭짓점에는 원자를 뜻하는 라벨도 붙어 있으므로 저 그래프는 라벨 그래프. (꼭짓점에 라벨이 붙어 있으면 라벨 그래프다) 4. 분자 그래프 구축 방식SMILES는 어쨌든 텍스트이기 때문에 그래프로 구축하려면 구축 과정을 거쳐야 한다.이는 마치 사람은 기계어가 모르고 컴퓨터는 사람의 말을 모르기 때문에 도중에서 프로그래밍 언어를 거치는 느낌.물론 기계어와 어셈블리 언어 사용자 수도 있다구축 방식은 명단과 인접 행렬로 나뉘지만 리스트는 정상별로 연결된 정점을 표 형태로 나열하는 방식이며, 인접 행렬은 정점으로 다른 정점의 연결 관계를 행렬로 나타낸 것이다.0라면 접속이 없는 것으로, 1는 접속된 것.상기예의 첫 탄소는 2번 탄소와 연결되어 있어 1개 2줄만 1이다.참고로 인접 항그랄의 주인 대각선은 자신과 루프로 이어지지 않는 이상 0이다.리스트 방식은 경로 파악이 빠른데, 연결 관계 파악에 시간이 오래 걸리고 인접 행렬 방식은 연결 관계 파악이 이른 것에 경로 파악에 시간이 걸린다.대체로 인공 지능 관련 논문에서는 인접 행렬을 사용하지만… 그렇긴리스트는 PDB파일에서 본 듯하다.